SISTEMAS LINEALES. Introducción.

En algunas ocasiones se presentan situaciones donde intervienen dos o más funciones lineales, cuyas incógnitas pueden estar relacionadas o no de alguna manera. Para la resolución de estas situaciones muchas veces conviene plantear su solución como un sistema de ecuación debido a la naturaleza de los datos.

Un sistema de ecuación lineal \(2\times2\) es un conjunto de dos ecuaciones lineales, las cuales se deben resolver de manera conjunta, en la forma: $$\left\{\begin{array}1ax+by=c\\mx+ny=d\end{array}\Longrightarrow \left\{\begin{array}1\mathrm{sistema~lineal~(mayor~exponente~uno)}\\\mathrm{Si~algún~exponente~es~distinto~de~ uno,~el~sistema~no~es~lineal.}\end{array}\right.\right.$$ Si el conjunto de ecuaciones está formado por tres ecuaciones con tres incógnitas se dice que es un sistema \(3\times3\), y así sucesivamente.

Resolución de un sistemas lineal.

Resolver un sistema de ecuación es determinar los valores de las incógnitas que hacen verdaderas todas las ecuaciones del sistema, llamado conjunto solución.

El conjunto solución si existe, está formado por el o los puntos de intersección de las rectas (ecuaciones).

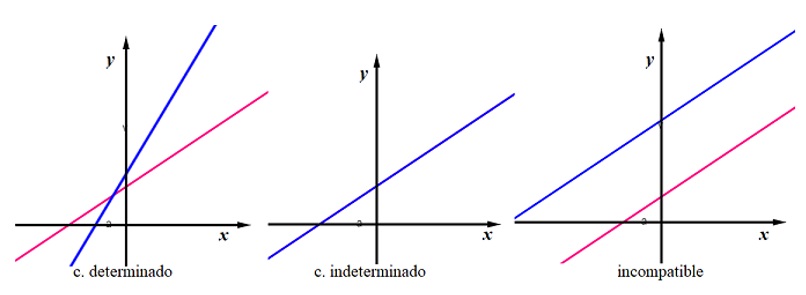
Si la solución del sistema es única, se dice que el sistema es compatible determinado y su representación gráfica son dos rectas que se intersecan en un punto del plano. Si las soluciones son infinitas se dice que el sistema es compatible indeterminado y su representación gráfica son dos rectas coincidentes (una encima de la otra). Si no posee solución se dice que es incompatible y su representación gráfica son dos rectas paralelas.

Métodos de resolución.

Al resolver un sistema de ecuación se puede utilizar diversos métodos para determinar los valores de las incógnitas que hacen verdaderas las ecuaciones del sistema, y para esto existen los llamados métodos de resolución, el método a utilizar dependerá de la destreza y/o especificación de cada situación.

Para este momento se presentan los métodos de eliminación por sustitución, eliminación por igualación, eliminación por reducción y el método gráfico, aunque cabe destacar que también existen otros métodos más avanzados como son el método matricial; uso de matrices inversas, por determinantes; el método de Gauss y de Gauss-Jordan, entre otros, para un curso de álgebra elemental se estudian los primeros cuatro mencionados, lo demás se ven en grados superiores.

Para ver uno de los métodos de resolución de un sistema de ecuación haga clic en el tema de preferencia del menú de la izquierda.